I det här inlägget ska vi:
- Gå igenom vad multikollinearitet är
- Gå igenom hur man upptäcker multikollinearitet
I tidigare inlägg har vi gått igenom hur man genomför regressionsanalys. I en serie inlägg tänkte jag ta upp regressionsdiagnostik, det vill säga hur man undersöker om regressionsmodellen är bra och tillförlitlig. Det första inlägget handlar om multikollinearitet.
Vad är multikollinearitet?
Enkelt uttryckt kan man säga att multikollinearitet är när två eller flera av de oberoende variablerna i regressionsmodellen är korrelerade med varandra i hög utsträckning. Det är ett problem för att man då inte kan hålla isär effekterna av de två variablerna på den beroende variabeln.
Låt oss säga att vi vill undersöka om en persons förtroende för olika EU-institutioner påverkar hur nöjd man är med demokratin i EU. Personer som har stort förtroende för EU-kommissionen förväntas vara mer nöjda med demokratin i EU än personer som har litet förtroende för EU-kommissionen. På samma sätt förväntas personer som har stort förtroende för Europaparlamentet vara mer nöjda med demokratin i EU än de som har litet förtroende för Europaparlamentet.
Det som kan vara problematiskt är dock att de som känner stort förtroende för EU-kommissionen också antagligen känner stort förtroende för Europaparlamentet – de två variablerna är korrelerade. Det blir då svårt att hålla isär vad det är som egentligen gör att man är nöjd med demokratin i EU.
Hur upptäcker man multikollinearitet?
Låt oss pröva vårt exempel. Vi använder data från SOM-undersökningen 2004, där frågor ställts både om förtroende för EU-kommissionen och EU-parlamentet, samt om nöjdhet med demokratin i EU. Den beroende variabeln är en skala från 1-4, där 4 betyder ”Mycket nöjd med demokratin i EU” och 1 betyder ”Inte alls nöjd med demokratin i EU”. De oberoende variablerna är skalor från 1-5 där 1 betyder ”Mycket litet förtroende” och 5 betyder ”Mycket stort förtroende”.
I tabell 1 nedan redovisas resultatet från tre regressioner (i det här inlägget förklaras hur man ska tolka regressionstabeller). I den första ingår bara förtroende för EU-kommissionen som oberoende variabel. I den andra är förtroende för Europaparlamentet den enda oberoende variabeln. I den tredje ingår båda variablerna.
Vi ser i modell 1 och 2 att både förtroende för EU-kommissionen och Europaparlamentet har positiva effekter på nöjdhet med demokratin i EU. Personer som är ett steg nöjdare med EU-komissionen förväntas vara 0,458 steg nöjdare med demokratin i EU; personer som är ett steg nöjdare med Europaparlamentet förväntas vara ett 0,466 steg nöjdare med demokratin i EU.
Men i modell 3, där båda variablerna ingår, har effekterna av båda variablerna minskat ordentligt, och ungefär halverats. Vi ser också att standardfelen (talen inom parentes) har ökat, och mer än fördubblats. Vi kan alltså vara mindre säkra på koefficienterna, även om de fortfarande är signifikanta på 95-procentsnivån. Kan multikollinearitet vara en orsak?
Det finns två huvudsakliga sätt att undersöka om regressionsmodellen lider av multikollinearitetsproblem. Det enklaste (och därmed kanske bästa) sättet är helt enkelt att undersöka korrelationerna mellan de oberoende variablerna. Resultatet från korrelationsanalysen visas i bild 1.
Bild 1. Korrelation mellan de båda oberoende variablerna.
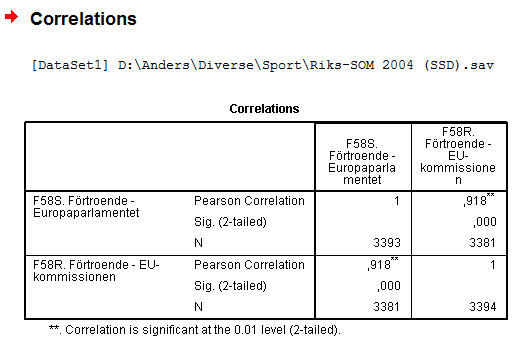
Korrelationen mellan de båda variablerna är mycket stark, 0,918. Som förväntat så har personer som har stort förtroende för den ena institutionen också stort förtroende för den andra institutionen.
Det är inte ovanligt att de oberoende variablerna korrelerar något. Hur mycket korrelation kan då anses som acceptabelt? Det finns inget definitivt värde, men när det går över ungefär 0,8 börjar det bli problematiskt. Vi kan alltså misstänka att koefficienterna i vår modell inte är tillförlitliga.
Men för att vara säkra kan vi också pröva med ett annat test. Vi gör då om regressionsanalysen, men klickar först på ”Statistics” och därefter klickar vi i rutan ”Collinearity diagnostics”, som i bild 2. Tryck därefter på ”Continue” och ”Ok”.
Bild 2. Hur man hittar collinearity diagnostics.
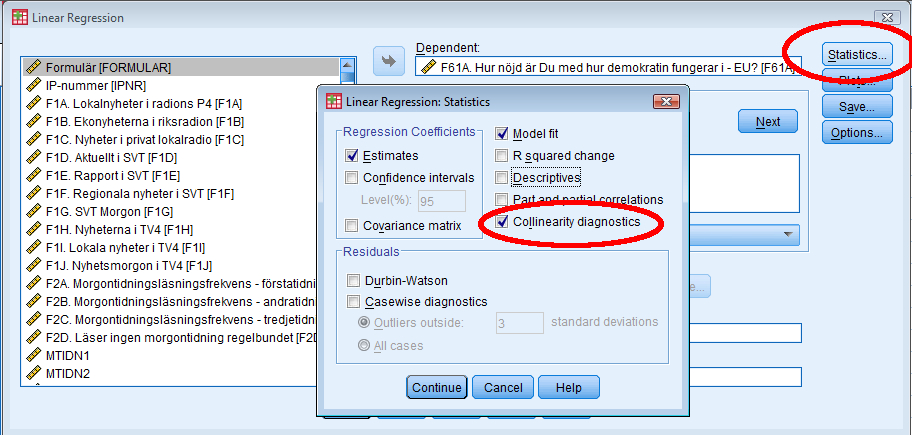
Man får ut den vanliga regressionsoutputen, men där man ser regressionskoefficienterna har det tillkommit en sektion längst till höger, ”Collinearity diagnostics”. Där visas två värden: ”Tolerance” och ”VIF”. VIF-värdet, som står för ”Variance Inflation Factor”, är helt enkelt 1 delat med ”Tolerance”-värdet. De säger alltså samma sak.
Bild 3. Hur man hittar multikollinearitetstestet i regressionsoutputen.
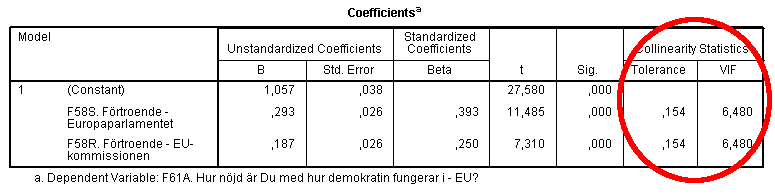
Tyvärr finns det inga exakta värden att gå på här heller, men jag brukar själv dra gränsen vid ett VIF-värde på 4, och det är en ganska vanlig gräns. Jag har också hört att vissa använder ett gränsvärde på 5. Motsvarande toleransvärden blir då 0,25 och 0,2. Man vill alltså att toleransvärdet ska vara så högt som möjligt (1 är max) och att VIF-värdet ska vara så lågt som möjligt (1 är minimum).
I vårt fall ser vi att VIF-värdet för de båda variablerna är 6,480, alltså mycket högt. Det beror på att de båda oberoende variablerna är så högt korrelerade. I det här fallet så blev effekterna signifikanta i alla fall, men ofta så leder multikollinearitet till att variabler som var för sig är signifikanta blir insignifikanta. Att det inte blev så i det här fallet beror antagligen på att det är många personer som ingår i analysen, över 3000. Det finns då tillräckligt många som har olika stort förtroende för EU-kommissionen och Europaparlamentet för att att vi ska kunna göra en analys.
Vad ska man då göra åt multikollinearitet? Eftersom de oberoende variablerna är så starkt korrelerade kan man säga att de mäter i princip samma sak. I vårt fall är det rimligt att tänka sig att de flesta inte särskiljer EU:s institutioner i särskilt hög utsträckning. Båda frågorna mäter då allmänt förtroende för EU:s institutioner. Man kan då argumentera för att det räcker med att ha med en av variablerna i analysen. Man skulle också kunna tänka sig att man gör ett index av de båda frågorna.


Hej! Tack för en superbra blogg!
Jag undrar vad ostandardiserad regressionskoefficient betyder? Närmare bestämt vad menas med ”ostandardiserad” när det gäller regressionskoefficienten? mvh Johanna
Hej och tack själv!’
Det betyder att koefficienten är effekten på den beroende variabeln av ett steg uppåt på den oberoende variabeln, uttryckt i den beroende variabelns skala. Om den beroende variabeln är mätt i centimeter, uttrycks koefficienten i centimeter.
Nackdelen med det är att det inte är lätt att jämföra styrkan på koefficienten för olika variabler. En variabel kanske går mellan 0 och 1, och en annan mellan 0 och 1000. Det kommer då antagligen att verka som att den senare variabeln har en mindre effekt.
Motsatsen är en standardiserad koefficient (beta). Koefficienten har då förändrats för att vara jämförbar – man har sett till att variansen är ett.
Man kan då jämföra styrkan på variabler mätta på olika skalor, men effekten går inte att tolka på samma sätt. Läs mer om det här:
http://en.wikipedia.org/wiki/Standardized_coefficient
/Anders
ps. Jag undrar även om t-värde alltid betyder testvärde?? Tacksam för svar. Ds
Njao, t-värdet är ett t-värde helt enkelt, t:et står inte för ”test”. Men t-värdet används alltid för att kontrollera om koefficienten är signifikant skild från ett visst värde (nästan alltid 0).
Du kan läsa mer om t-värdet här:
http://en.wikipedia.org/wiki/Student%27s_t-test
/Anders
Hej Anders
Tack för en bra blogg när man snabbt ska uppdatera sitt minne på regressionsanalys.
Jag håller på med och analyserar ett lönematerial med regressioner för att se om det finns oförklarade löneskillnader mellan könen. En viktig förklaringsfaktor för lönenivå är ju erfarenhet (i det här fallet översatt till ålder) och det är tydligt att det finns en sådan effekt i materialet.
Effekten brukar dock vara avtagande med åren (de första åren i arbetslivet höjs lönen kraftigare än de senare) vilket gör att man får en bättre (i meningen förklarar mer) ekvation om man stoppar in både lön och lön i kvadrat i ekvationen. (för att skriva det formelmässigt lön=a+b1*ålder+b2*ålder*ålder+konstant). I detta fall blir b1 positivt och b2 negativt.
Alla p-värden i beräkningarna är <.0001. Problemet är att de bägge VIF-värden för ålder blir över 18. Det finns alltså en rätt stor multikollinearitet mellan dem. Är det bara att utesluta det ena värdet eller går det att använda båda ändå?
Hej!
Kul att du gillar bloggen.
Du ska definitivt ha med båda variablerna. De är ju korrelerade per definition, så det är inte konstigt att multikollineariteten blir hög. Men det är inget att oroa sig för! Om du bara kör med den otransformerade så blir det ju en linjär funktion. Och kör du bara med den kvadrerade variabeln blir det väldigt konstigt. Så kör alltså med båda variablerna samtidigt!
/Anders
Hej!
Fick ett så himla bra svar av dig förra veckan, så jag provar att fråga igen!
Jag kör min regression med ganska många variabler och dessutom interaktionsvariabler på det. Då får jag meddelandet ”For models with dependent variable si och så the following variables are constants or have missing correlations. They will be deleted from the analysis ” Vad betyder detta, och vad kan jag göra åt det? Har kollat och ingen av variablerna har ett konstant värde. De ser dessutom okej ut när jag kollar korrelationen.
Och: två variabler har blivit exkluderade på grund av tolerance. Tyvärr är den ena (x1 låt säga) en av mina ”grundvariabler” för interaktionsvariablerna. Några av x1-interaktionerna är signifikanta och jag skulle vilja räkna ut deras effekter – men har ju inget värde på x1 vilket väl behövs!
Vore vääääldigt tacksam om du kunde reda ut detta! Tack för en grym sida.
Hej!
Det är svårt att säga, men det är antagligen så att några av dina variabler kan förutsäga några av de andra oberoende variablerna exakt. Ett exempel är när du har dummyvariabler för alla kategorier. Om du till exempel har en dummyvariabel för ”Man” och en för ”Kvinna” kommer en att uteslutas. Om man inte är man så är man garanterat kvinna (om man inte blir för queer-teoretiskt avancerad). Samma sak gäller om du till exempel har gjort en variabel som är skillnaden mellan två variabler. Typ om du har en variabel som är ”När blev du anställd på ditt senaste jobb” och ”När slutade du ditt senaste jobb” samt en variabel som är ”Hur länge jobbade du på ditt senaste jobb”. Vet man värdet på två av de variablerna vet man också värdet på den tredje, och då blir det perfekt multikollinearitet.
Skulle gissa att det är något i den stilen som är problemet! Bygg upp modellen steg för steg och se när det tar stopp.
/Anders
Hei!
Meget bra blogg! Er veldig ny på SPSS, men har fått en oppgave der vi skal teste multikollinaritet på 2 uavhengige variabler opp mot en avhenging variabel. Den ene uavhengige variablen er diktom, den andre uavhengige variablen er nominal. Hvordan måles multikollinaritet da? Hva er stegene i SPSS?
Hej Hilde!
Om den ena variabeln är en nominalskala så måste du göra om den till dummyvariabler om du ska kunna använda den i regressionsanalys (eller undersöka korrelationer). Så du gör om det till dummyvariabler och gör på samma sätt som jag beskriver i guiden ovan.
/Anders
Grundfeldt (2003) skriver att den beroende variabeln måste vara kvantitativ och ickebinär. Min lärare hävdar dock att det ändå finns fördelar med en multipel regressionsanalys (OLS) när min beroende variabel är inställning till brott (negativ, neutral eller positiv = ordinal = kvalitativ ?) Jag fick en artikel som stöd för detta som nu försvunnit och får inte tag i min lärare. Kan man argumentera för att den beroende variabeln inte måste vara kvantitativ? Om inte hur ska jag göra annars?
Hej!
De statistiska antagandena bygger på att variablerna är på intervallskalenivå. Men en regressionsanalys kan ändå säga någonting om sambandet mellan variablerna. men då bör du argumentera för att avstånden mellan variabelvärdena är lika stora. Jag har skrivit lite mer om det här:
https://spssakuten.wordpress.com/2010/03/14/lasarfraga-ordinalskalor-som-beroende-variabel/
/Anders
Hej Anders,
Jag håller på att skriva min masteruppsats i politik och internationella studier. Jag har en fråga till dig som rör signifikanser och eventuella multikollinearitetsproblem. Jag har ett dataset bestående av 600 fall, med en beroende variabeln på intervallskala (antal dagar). När jag testar en av de oberoende variablerna genom bivariat regression påvisas ingen signifikant effekt (p=0,25). Vid multivariat körning tillsammans med en av de övriga oberoende variablerna, och tillsammans med samtliga övriga variabler, fördubblas effekten och den är plötsligt signifikant (p=0,02); alltså tvärtom mot hur det brukar kunna vara.
När jag testar korrelationen mellan den ”problematiska” variabeln och den andra oberoende variabeln framgår förvisso att det finns ett signifikant samband mellan dem (Pearson= -0,322), men tolerans- och VIF-värdena i den multivariata regressionen anger inte att det föreligger multikollinearitet (tolerans=0,92 och VIF=1,1).
Alltså, effekten av variabeln är inte signifikant i bivariat analys, men i multivariat.
Vad kan detta bero på? Och hur ska jag tackla det?
Tack för en fantastisk blogg med mycket matnyttig information och tips!
Hej Oskar!
Det ”vanliga” är att man hittar ett samband i en bivariat analys, som sedan försvinner under kontroll för en annan variabel. Det beror då oftast på att kontrollvariabeln är positivt korrelerad med både den beroende och den oberoende variabeln, eller negativt korrelerad med både den beroende och den oberoende variabeln.
I ditt fall är det tvärtom. Det kan bli så när kontrollvariabeln är positivt korrelerad med den oberoende variabeln, och negativt korrelerad med den beroende variabeln, eller tvärtom. I såna fall kommer det okontrollerade sambandet mellan den beroende och den oberoende variabeln att vara ”undertryckt”.
Jag föreslår att du kollar upp de bivariata korrelationerna mellan alla dina variabler. Jag skulle gissa att det ligger till på sättet som jag beskrev.
En mycket bra bok som diskuterar de här sakerna är Aneshensels ”Theory-based data analysis for the social sciences.”
http://books.google.se/books/about/Theory_based_data_analysis_for_the_socia.html?id=3uXvdOhp2YkC&redir_esc=y
/Anders
Hej Anders!
Tack för en finfin blogg! Jag har en fråga som rör multikollinearitet – jag har en mycket stor datamängd (21000 observationer) där jag har upptäckt multikollinearitet mellan två av de förklarande variablerna. De har ett korrelationsvärde på 0,957 och VIF på 12. Men när jag kör regressionsanalysen blir ändå alla regressionskoefficienter signifikanta (p mycket nära 0)? Vad kan detta bero på? Kan man anta att modellen och dess koefficienter ändå stämmer trots att multikollinearitet verkar förekomma? Båda de förklarande variablerna är viktiga för modellen, så utesluta en utav dem är ingen riktigt bra lösning tyvärr. Finns det något annat sätt att komma runt problemet (om det nu är ett problem vill säga) med multikollinearitet än att utesluta en av variablerna?
Tack på förhand!
Jag har en snabb fråga, vi har en modell med 10 oberoende variabler och när jag gör en korrelation matrix ser jag att två av de korrelerar högt (0,859), medan när jag kör VIF testet får jag fram att de inte korrelerar med varandra. Vad kan detta bero på?
MVh Carolina Einarsson
Hej,
Tack för en otroligt bra förklaring, textenvar både tydliga och pedagogiska och jag uppskattar det verkligen! Klara
Tusen tack för en tydlig förklaring. Som ny student inom samhällsvetenskapliga ämnet var detta toppen!